Note: I enjoy working with numbers (this page) and playing with words (this link).

Table /Maker Five   Email: roizen@ix.netcom.com
Math recipes with fresh ideas and free delivery!

    

Sketch from Programmers At Work, Microsoft Press, (c) 1983

This product has its roots in one I created in 1979 and another in 1991 (i.e., ancient PC history). In January (2020)
an automatic Windows update destroyed the XP partition where I could still enjoy these tools. Well, I could not bring
myself to use a traditional spreadsheet. This approach has met all my math needs for the last 40 years. So I decided
to unretire and create an update incorporating advances in equipment and development environments as well as
modernizing the interface. You are welcome to add T/Maker to your Mac or Windows menu.

T/Maker offers the ease of use and conceptual simplicity of a hand calculator over two dimensions. Many may never
use it for more than arithmetic across rows and columns, but that is what most people do most of the time.

References: https://en.wikipedia.org/wiki/Peter_Roizen       https://en.wikipedia.org/wiki/T/Maker

Being perfectly blunt:

I find algebraic formulae: tedious, mistake prone,  too much typing, and a constant reminder of Bingo.

I find calculation trails in separate cells: intuitive, quick, and  fun!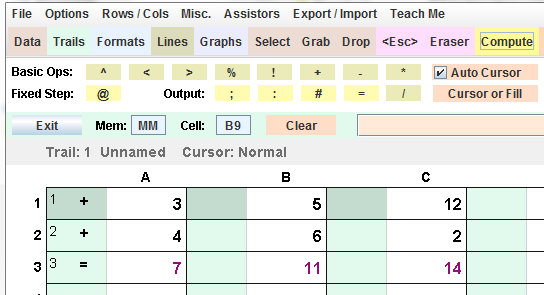

"And wait," as they say on infomercials, "there is even more!" Please don't jump to any conclusions yet.

T/Maker is a java desktop application for Mac and Windows computers. It makes no connection to the internet
when used. There is no self-updating, tracking, ads, or any sort of pestering or spying. All your data is kept on
your machine. It should run for the next 30 years under java. I will not be doing any marketing. I do hope some
adventurous souls who happen onto this page will give T/Maker a try and find it useful in their lives. And if so,
I hope they will pass the link on. Feedback is always welcomed.

Links for later:  The Download Page      Tutorial Videos      Example Tables

The videos are amateurish and one day I will redo them. But luckily T/Maker is easy to grasp and you can put it to
work after a few minutes. I want to move on to redoing my word game which will appeal to a wider audience.

If you have a touch screen (Windows 10),  it is amazing what you can do with T/Maker using just one finger while
on the sofa. Of course, everything can be done with a keyboard along with a mouse or touch pad.

Click for touch screen video.

This one uses a mouse. There is some overlap with the above but fresh material as well. Video 1

I would like to say a few serious words about learning math with T/Maker. Students who know arithmetic can build
their problem solving skills along with an introduction to data analysis, statistics, logic, and graphics years before the
7th or 8th grade. And that will help close the thinking gap between apples and oranges arithmetic and algebra.
That's a leap that comes out of nowhere and many have difficulty accomplishing it.  Building confidence and feeling
comfortable using math to solve problems is a T/Maker specialty. It's also what math educators say about getting
better at math--USE IT !  Kids can do it for their own problems with a tad of help getting started.



The image below shows elements you may use when building calculation trails. There are a few notations here that are particular
to T/Maker's approach and fit well with it. But much is just the application of basic arithmetic with operators, constants, memories,
and functions you could do with a variety of hand calculators. However,  that would be incredibly more laborious, and you would
have no record of what you specified. You don't need to learn what you don't need to use.


Video 2: The syntax is on the table


Memories, I should point out, introduce the notion of names or letters representing values (algebra) under the easiest to understand
circumstances. You pick the name and you put the value in it. Memories also provide incredible economies in specifications.
Here are 48 values calculated by one simple trail. This is practical math taken to a whole new level.

Video 3: Memories are made for this


The Combo Cursor is a cursor that performs a variety of calculations as it proceeds in a trail and stores the results in memories
where they can be easily fetched. Among the values are the minimum, the maximum, the mean, and the median. These
are some elementary members of what you might call statistics and data analysis. There's a standard deviation too and an
example table of calculating a correlation coefficient. The  video also includes changing some formats, a sort, and making
a stacked bar chart. It's all easy.

Video 4: A multi-tasking cursor




One of the very nice things about T/Maker is that it
can clone rows incorporating all elements of a model
row. Many tables have a block or blocks of rows that
are identical in terms of the calculations and other
elements they require. This feature is great for building
a table over time.

Video 5: Another row for the road







As a programmer, I know that no syntax or language is complete without a tool to debug the work
you have done. Here's is one for T/Maker's unusual way of writing calculations. It's a way to find
mistakes or just review how things work and fit together.


Video 6: A walkabout on trails




I want to nip in the bud the notion that T/Maker might be only a toy suitable
for youngsters by showing (without a lot of explanation) a table that runs a
simulation of the optimal strategy for playing roulette. That strategy works from
the amount you want to risk and what your want to win. It bets on single numbers
with increasing bets until you go broke or hit one number. At your first win, you
have achieved your goal. It also allows me to make some meaningful contrasts
between trails (T/Maker) and formulae (spreadsheets).

Video 7: Yes, I can!






Before getting back to more meat on how you contsruct and use trails, I did want you to see that you can import
and export data to other cell based programs or even pick data up from web pages in some cases. This might
hopefully encourage you to try T/Maker since you can start with data you already have or transfer data from
T/Maker to another program if so inclined.


Video 8: Well, Hello Data!


You have already seen the Lite Assistor for trails, this video explains its big brother.


Note that the math functions are there to tackle geometry, trigonometry,  exponentials,  logarithms, and there is a random number
generator for simulations.  Mortage payments, present value, and growth rates are also built in with an easy to use approach.

Video 9: Big Brother



I wanted to show you one other assistor that is handy if a logical test is needed to direct calculations that should
only be done under certain conditions. It's called a WHEN clause. In the video you will see how to construct one
and another usage which can be handy for finding data entry errors or just counting instances of various values
in a column of a table.


Video 10: When WHEN


I would not say entering and editing data is much different from other cell based programs. But you will
see a nifty way to get to locations in your table or make use of abbreviations.


Video 11: A little gift for terrible typists


While the charts and graphs are not on a par with well-established spreadsheets, you can use them to get insights into your data
and a student can learn what type of chart best illustrates a certain point.



You can easily print your tables. Here is the print box for that. It tells you how many pages wide and pages long it
will be. You can reset the parameters that affect the size and recalculate. If you are just interested in keeping historical
paper records, you can save paper and ink this way. You can  also make some nice forms, not that I want to contribute
to the number of forms in the world though I would like more space to actually write the address! Here's a (scanned)
invoice printed with some lines and a typo.
.

   

I believe T/Maker is easy to learn and hard to forget. The tools you will need for various tasks are at the top of the screen, so you won't
have to search for them in pop-up or drop down boxes. The interface is consistent across all  functions/screens.  You will find it
worth firing up for even just a few numbers and calculations.

Here again are the links to the download page and other information. And thank you for your time and attention.

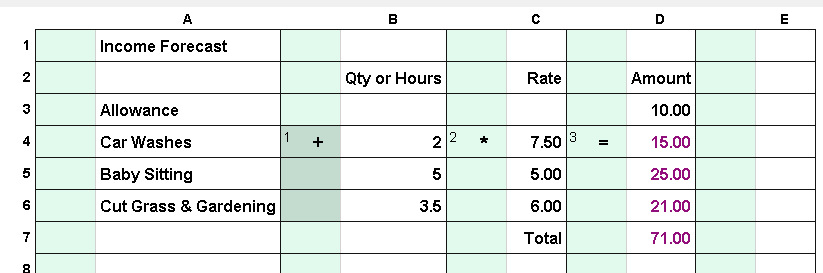
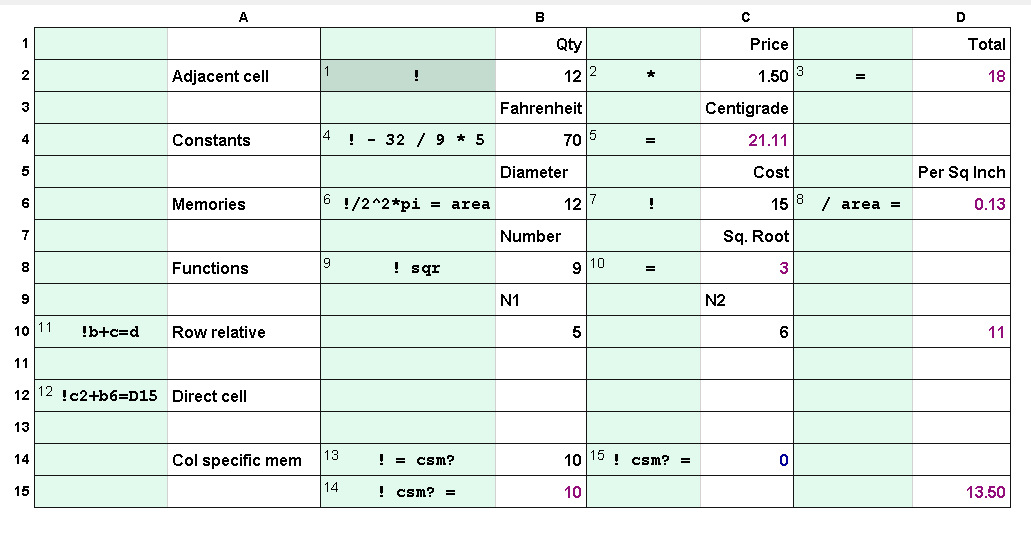
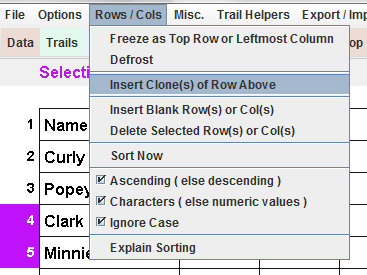
Links:  The Download Page      Tutorial Videos      Example Tables

Key Words and Phrases: Simple easy spreadsheet, easy simple spreadsheet, amazing, inexpensive, cheap, T/Maker, table maker, two dimensional calculator, arithmetic based, no algebra, straightforward, iterations, goal seeking, applications, programmable, fewer mistakes, not error prone, pleasant look and feel, consistent, efficient, common problems, mortgage payment, growth rate, present value, blackboard, green board, white board, elementary school, multiplication tables, division tables, middle school, high school, kids, children, adults, home schooling, math skills, add, subtract, divide, multiply, subtraction, division, multiplication, learning, memories, fun, unconventional, wonderful syntax options, power and ease, make your own templates, home budgeting, home finance, cash flow, invoices, project estimates,
household templates spreadsheet for the whole family, unique, the unspreadsheet spreadsheet, DIY projects, science projects, home accounting, one of a kind.